问题
计算题
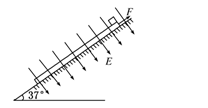
(12分)如图11所示，长L＝1.2 m、质量M＝3 kg的木板静止放在倾角为37°的光滑斜面上，质量m＝1 kg、带电荷量q＝＋2.5×10－4 C的物块放在木板的上端，木板和物块间的动摩擦因数μ＝0.1，所在空间加有一个方向垂直斜面向下、场强E＝4.0×104 N/C的匀强电场．现对木板施加一平行于斜面向上的拉力F＝10.8 N. 取g＝10 m/s2，斜面足够长．求：
(1)物块经多长时间离开木板？
(2)物块离开木板时木板获得的动能．
(3)物块在木板上运动的过程中，由于摩擦而产生的内能．
答案
(1)
s (2)27 J (3)2.16 J
(1)物块向下做加速运动，设其加速度为a1，木板的加速度为a2，则由牛顿第二定律
对物块：mgsin37°－μ(mgcos37°＋qE)＝ma1
对木板：Mgsin37°＋μ(mgcos37°＋qE)－F＝Ma2
又
a1t2－a2t2＝L
得物块滑过木板所用时间t＝ s.
(2)物块离开木板时木板的速度v2＝a2t＝3 m/s.
其动能为Ek2＝Mv22＝27 J
(3)由于摩擦而产生的内能为
Q＝F摩x相＝μ(mgcos37°＋qE)·L＝2.16 J.