依题意：（1）当a=0时，f（x）=x³，在（-∞，+∞）上为增函数，有一个单调区间     ①

当a≠0时，∵f（x）=x³+a|x²-1|a∈R

∴f（x）=

x3+ax2-a   x∈(-∞，-1]∪[1，+∞) x3-ax2+a   x∈(-1，1)

∴f′（x）=

3x2+2ax   x∈(-∞，-1]∪[1，+∞) 3x2-2ax    x∈(-1，1)

（2）当0＜a＜

3

2

时，∵-

1

2

＜-

a

3

＜0，0＜

a

3

＜

1

2

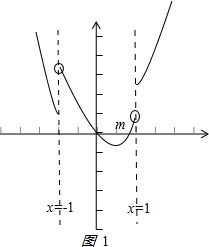
，∴导函数的图象如图1：（其中m为图象与x轴交点的横坐标）

∴x∈（-∞，0]时，f′（x）＞0，x∈（0，m）时，f′（x）＜0，x∈[m，+∞）时，f′（x）＞0，

∴f（x）在x∈（-∞，0]时，单调递增，x∈（0，m）时，单调递减，x∈[m，+∞）时，单调递增，有3个单调区间    ②

（3）当a≥3时，∵-

a

3

＜-1，

a

3

＞1，∴导函数的图象如图2：

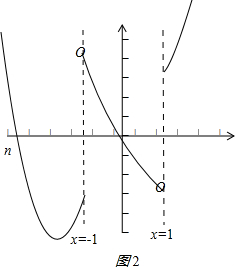
（其中n为x≤-1时图象与x轴交点的横坐标）

∴x∈（-∞，n]时，f′（x）＞0，x∈（n，-1]时，f′（x）＜0，x∈（-1，0）时，f′（x）＞0，x∈[0，1）时，f′（x）＜0，x∈[1，+∞）时，f′（x）＞0

∴函数f（x）在x∈（-∞，n]时，单调递增，x∈（n，-1]时，单调递减，x∈（-1，0）时，单调递增，x∈[0，1）时，单调递减，x∈[1，+∞）时，单调递增，

有5个单调区间       ③

由①②③排除A、C、D，

故选B