问题
计算题
如图甲所示，在两平行金属板的中线OO′某处放置一个粒子源，粒子沿OO1方向连续不断地放出速度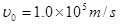
的带正电的粒子。在直线MN的右侧分布有范围足够大的匀强磁场，磁感应强度B=0.01
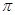T，方向垂直纸面向里，MN与中线OO′垂直。两平行金属板间的电压U随时间变化的U—t图线如图乙所示。已知带电粒子的荷质比
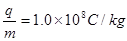，粒子的重力和粒子之间的作用力均可忽略不计，若
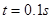时刻粒子源放出的粒子恰能从平行金属板边缘离开电场（设在每个粒子通过电场区域的时间内，可以把板间的电场看作是恒定的）。求：
（1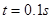）时刻粒子源放出的粒子离开电场时的速度大小和方向。
（2）从粒子源放出的粒子在磁场中运动的最短时间和最长时间。
答案
（1）
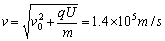θ＝45°（2）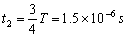
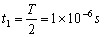
题目分析：（1）设板间距为d，t＝0.1s时刻释放的粒子在板间做类平抛运动
在沿电场方向上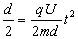
①
粒子离开电场时，沿电场方向的分速度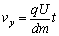
②
粒子离开电场时的速度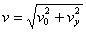 
③
粒子在电场中的偏转角为θ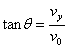 
④
由①②③④得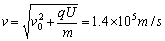
θ＝45°
说明：用
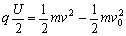和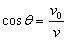
联立求出正确结果，参照上述评分标准给分。
（2）带电粒子在匀强磁场中做匀速圆周运动的周期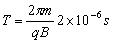
不同时刻释放的粒子在电场中的偏转角θ不同，进入磁场后在磁场中运动的时间不同，θ大的在磁场中的偏转角大，运动时间长。
t＝0时刻释放的粒子，在电场中的偏转角为0，在磁场中运动的时间最短：
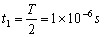
t＝0.1s时刻释放的粒子，在电场中的偏转角最大为45°，在磁场中运动的时间最长：
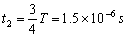
点评：本题关键是画出粒子进入磁场后的各种可能的运动轨迹，根据洛伦兹力提供向心力列式后得出半径，然后求出磁偏转的距离表达式，并得出回旋角度的范围，从而得到磁偏转的范围．
