函数f（x）的定义域为（0，+∞），…（1分）

（Ⅰ）f′(x)=

x2+ax-2a2

x

=

(x+2a)(x-a)

x

，…（4分）

（1）当a=0时，f'（x）=x＞0，所以f（x）在定义域为（0，+∞）上单调递增； …（5分）

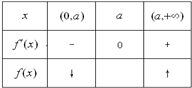
（2）当a＞0时，令f'（x）=0，得x₁=-2a（舍去），x₂=a，

当x变化时，f'（x），f（x）的变化情况如下：

此时，f（x）在区间（0，a）单调递减，

在区间（a，+∞）上单调递增；          …（7分）

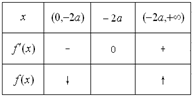
（3）当a＜0时，令f'（x）=0，得x₁=-2a，x₂=a（舍去），

当x变化时，f'（x），f（x）的变化情况如下：

此时，f（x）在区间（0，-2a）单调递减，

在区间（-2a，+∞）上单调递增．…（9分）

（Ⅱ）由（Ⅰ）知当a＜0时，f（x）在区间（0，-2a）单调递减，在区间（-2a，+∞）上单调递增．…（10分）

（1）当-2a≥e，即a≤-

e

2

时，f（x）在区间[1，e]单调递减，

所以，[f(x)]min=f(e)=-2a2+ea+

1

2

e2；                     …（11分）

（2）当1＜-2a＜e，即-

e

2

＜a＜-

1

2

时，f（x）在区间（1，-2a）单调递减，

在区间（-2a，e）单调递增，所以[f(x)]min=f(-2a)=-2a2ln(-2a)，…（12分）

（3）当-2a≤1，即-

1

2

≤a＜0时，f（x）在区间[1，e]单调递增，

所以[f(x)]min=f(1)=a+

1

2

．…（13分）