问题
填空题
设函数f(x)=
|
答案
f′(x)=x2-ax+(2-b)
∵两个极值点一个在区间(0,1)内,另一个在区间(1,2)内
∴
即f′(0)>0 f′(1)<0 f′(2)>0 2-b>0 a+b-3>0 2a+b-6<0
画出可行域
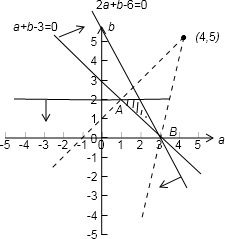
表示的是可行域中的点与(4,5)连线的斜率b-5 a-4
由图知当直线过A((1,2)时斜率最小;当直线过B(3,0)时,斜率最大
kmin=
=1,kmax=5-2 4-1
=55 4-3
