（1）由题意f′（x）=x²-（k+1）x，

因为f（x）在区间（2，+∞）上为增函数，

所以f′（x）=x²-（k+1）x≥0在（2，+∞）上恒成立，即k+1≤x恒成立，

又x＞2，所以k+1≤2，故k≤1，

当k=1时，f′（x）=x²-2x=（x-1）²-1在x∈（2，+∞）恒大于0，故f（x）在（2，+∞）上单增，符合题意．

所以k的取值范围为k≤1．

（2）设h(x)=f(x)-g(x)=

x3

3

-

(k+1)

2

x2+kx-

1

3

，

h′（x）=x²-（k+1）x+k=（x-k）（x-1），

令h′（x）=0得x=k或x=1，由（1）知k≤1，

①当k=1时，h′（x）=（x-1）²≥0，h（x）在R上递增，显然不合题意；

②当k＜1时，h（x），h′（x）随x的变化情况如下表：

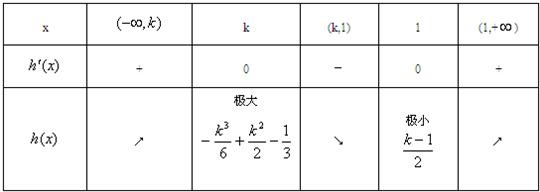
由于

k-1

2

＞0，欲使f（x）与g（x）图象有三个不同的交点，

即方程f（x）=g（x），也即h（x）=0有三个不同的实根．

故需-

k3

6

+

k2

2

-

1

3

＞0即（k-1）（k²-2k-2）＜0，

所以

k＜1 k2-2k-2＞0

，解得k＜1-

3

．

综上，所求k的范围为k＜1-

3

．