问题
选择题
已知α,β是三次函数f(x)=
|
答案
∵函数f(x)=
x3+1 3
ax2+2bx1 2
∴f′(x)=x2+ax+2b
又∵α∈(0,1),β∈(1,2),
∴f′(0)=2b>0 f′(1)=1+a+2b<0 f′(2)=4+2a+2b>0
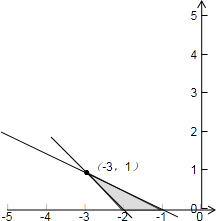
其对应的平面区域如下图所示:
由图可得:当x=-3,y=1时,
取最小值b-2 a-1
;1 4
当x=-1,y=0时,
取最大值1;b-2 a-1
故选A
