已知函数f(x)=
(1)求函数f(x)的单调区间; (2)若关于x的不等式lnx<mx对一切x∈[a,2a](其中a>0)都成立,求实数m的取值范围; (3)某同学发现:总存在正实数a、b(a<b),使ab=ba.试问:他的判断是否正确?若不正确,请说明理由;若正确,请写出a的取值范围(不需要解答过程). |
(1)定义域为(0,+∞),f′(x)=
,令f′(x)=1-lnx x2
=0,则x=e,1-lnx x2
当x变化时,f'(x),f(x)的变化情况如下表:

∴f(x)的单调递增区间为(0,e);f(x)的单调递减区间为(e,+∞).(4分)
(2)∵不等式lnx<mx对一切x∈[a,2a](其中a>0)都成立,
∴分离m得,m>
对一切x∈[a,2a](其中a>0)都成立,lnx x
∴下面即求f(x)=
在x∈[a,2a](其中a>0)上的最大值;lnx x
∵a>0,由(2)知:f(x)在(0,e)上单调递增,在(e,+∞)上单调递减.
当2a≤e时,即0<a≤
时,f(x)在[a,2a]上单调递增,∴f(x)max=f(2a)=e 2
;ln2a 2a
当a≥e时,f(x)在[a,2a]上单调递减,∴f(x)max=f(a)=
;lna a
当a<e<2a时,即
<a<e时,f(x)在[a,e]上单调递增,f(x)在[e,2a]上单调递减,e 2
∴f(x)max=f(e)=
.1 e
综上得:
当0<a≤
时,m>f(2a)=e 2
;ln2a 2a
当a≥e时,m>f(a)=
;lna a
当
<a<e时,m>f(e)=e 2
.(12分)1 e
(3)正确,a的取值范围是1<a<e.(16分)
注:理由如下,考虑函数f(x)的大致图象.
当x→+∞时,f(x)→0.
又∵f(x)在(0,e)上单调递增,在(e,+∞)上单调递减,∴f(x)的图象如图所示.
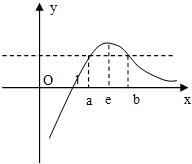
∴总存在正实数a、b且1<a<e<b,使得f(a)=f(b),
即
=lna a
,即ab=ba,此时1<a<e.lnb b
