问题
计算题
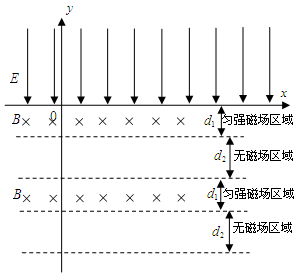
（12分）如图所示，在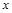
轴上方有一竖直向下的匀强电场区域，电场强度为
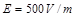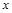。轴下方分布有很多磁感应强度为
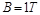的条形匀强磁场区域，其宽度均为为
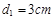，相邻两磁场区域的间距为
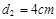。现将一质量为
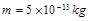、电荷量为
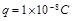的带正电的粒子（不计重力）从
轴上的某处静止释放。
（1）若粒子从坐标（0,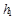
）点由静止释放，要使它经过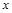轴下方时，不会进入第二磁场区，
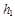应满足什么条件？
（2）若粒子从坐标（0,
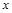）点由静止释放，求自释放到第二次过轴的时间。
答案
（1）
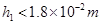（2）
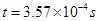
题目分析：(1)粒子经电场加速，经过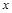
轴时速度大小为
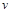，满足：
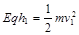
之后进入下方磁场区，依据题意可知运动半径应满足：
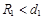
又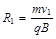
由以上三式可得：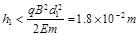
（2）当粒子从
的位置无初速释放后，先在电场中加速，加速时间为
满足
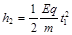
解得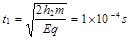
进入磁场的速度大小为
，圆周运动半径为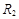
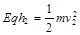
解得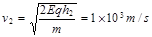
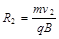
解得：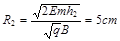
根据粒子在空间运动轨迹可知，它最低能进入第二个磁场区，它在磁场区共运动时间为半个圆周运动的时间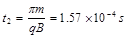
，经过第一无磁场区时运动方向与轴的夹角
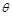满足：
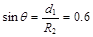
所以它在无磁场区的路程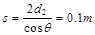
无磁场区运动时间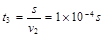
总时间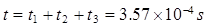
点评：该题是一道综合性较强的题，主要是考察了带电粒子在电场中的加速、偏转和在磁场的匀速圆周运动．解决此类问题常用的方法是对过程进行分段，对各个段内的运动情况进行具体分析，利用相关的知识进行解答．这要求我们要对带电粒子在电场和磁场中的运动规律要了如指掌，尤其是带电粒子在磁场中的偏转，确定轨迹的圆心是解决此类问题的关键．