（1）由已知得f′（x）=ax²+2bx+1，

令f′（x）=0，得ax²+2bx+1=0，

f（x）要取得极值，方程ax²+2bx+1=0，必须有解，

所以△=4b²-4a＞0，即b²＞a，

此时方程ax²+2bx+1=0的根为

x₁=

-2b- 4b2-4a

2a

=

-b- b2-a

a

，x₂=

-2b+ 4b2-4a

2a

=

-b-+ b2-a

a

，，

所以f′（x）=a（x-x₁）（x-x₂）

当a＞0时，

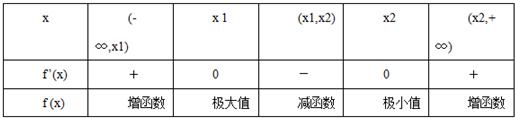
所以f（x）在x1，x2处分别取得极大值和极小值．

当a＜0时，

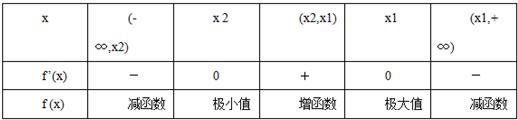
所以f（x）在x1，x2处分别取得极大值和极小值．

综上，当a，b满足b²＞a时，f（x）取得极值．

（2）要使f（x）在区间（0，1]上单调递增，需使f′（x）=ax²+2bx+1≥0在（0，1]上恒成立．

即b≥-

ax

2

-

1

2x

，x∈（0，1]恒成立，

所以b≥-(-

ax

2

-

1

2x

) max

设g（x）=-

ax

2

-

1

2x

，g′（x）=-

a

2

+

1

2x2

=

a(x2- 1 a )

2x2

，

令g′（x）=0得x=

1

a

或x=-

1

a

（舍去），

当a＞1时，0＜

1

a

＜1，当x∈（0，

1

a

]时g′（x）＞0，g（x）=-

ax

2

-

1

2x

单调增函数；

当x∈（

1

a

，1]时g′（x）＜0，g（x）=-

ax

2

-

1

2x

单调减函数，

所以当x=

1

a

时，g（x）取得最大，最大值为g（

1

a

）=-

a

．

所以b≥-

a

当0＜a≤1时，

1

a

≥1，

此时g′（x）≥0在区间（0，1]恒成立，

所以g（x）=-

ax

2

-

1

2x

在区间（0，1]上单调递增，当x=1时g（x）最大，最大值为g（1）=-

a+1

2

，

所以b≥-

a+1

2

综上，当a＞1时，b≥-

a

；

0＜a≤1时，b≥-

a+1

2

；