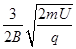问题
计算题
如图所示，两平行金属板E、F之间电压为U，两足够长的平行边界MN、PQ区域内，有垂直纸面向外的匀强磁场，磁感应强度为B.一质量为m、带电量为+q的粒子（不计重力），由E板中央处静止释放，经F板上的小孔射出后，垂直进入磁场，且进入磁场时与边界MN成60°角，最终粒子从边界MN离开磁场.求：
（1）粒子离开电场时的速度大小v；
（2）粒子在磁场中圆周运动的半径r和运动的时间t.
（3）两边界MN、PQ的最小距离d；
答案
（1）
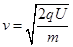（2）4
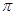m/3qB（3）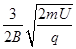
题目分析：（1）设粒子离开电场时的速度为v，由动能定理有：qu=mv2/2
解得：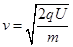
（2）粒子离开电场后，垂直进入磁场，由洛仑兹力提供向心力有：qBv= mv2/r
联立解得：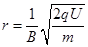
粒子在磁场中做圆周运动的周期T=2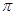r/v
联立解得：T=2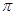m/qB
粒子在磁场中运动的时间t=2400/3600 T=4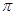m/3qB
（3）最终粒子从边界MN离开磁场，需满足：d≧r+rsin300
联立④⑤解得：d≧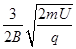
两边界MN、PQ的最小距离d为