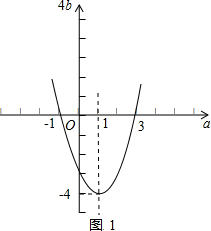问题
解答题
阅读下列材料:
题目:已知实数a,x满足a>2且x>2,试判断ax与a+x的大小关系,并加以说明.
思路:可用“求差法”比较两个数的大小,先列出ax与a+x的差y=ax-(a+x),再说明y的符号即可.
现给出如下利用函数解决问题的方法:
简解:可将y的代数式整理成y=(a-1)x-a,要判断y的符号可借助函数y=(a-1)x-a的图象和性质解决.
参考以上解题思路解决以下问题:
已知a,b,c都是非负数,a<5,且a2-a-2b-2c=0,a+2b-2c+3=0.
(1)分别用含a的代数式表示4b,4c;
(2)说明a,b,c之间的大小关系.
答案
(1)∵a2-a-2b-2c=0,a+2b-2c+3=0,
∴
,2b+2c=a2-a 2c-2b=a+3
消去b并整理,得4c=a2+3.
消去c并整理,得4b=a2-2a-3.
(2)∵4b=a2-2a-3=(a-3)(a+1)=(a-1)2-4,
将4b看成a的函数,由函数4b=(a-1)2-4的性质结合它的图象(如图1所示),
以及a,b均为非负数得a≥3.
又∵a<5,
∴3≤a<5.
∵4(b-a)=a2-6a-3=(a-3)2-12,
将4(b-a)看成a的函数,由函数4(b-a)=(a-3)2-12的性质结合它的图象
(如图2所示)可知,当3≤a<5时,4(b-a)<0.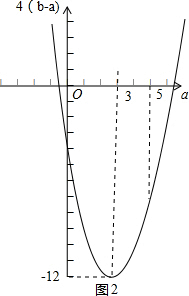
∴b<a.
∵4(c-a)=a2-4a+3=(a-1)(a-3),a≥3,
∴4(c-a)≥0.
∴c≥a.
∴b<a≤c.