问题
解答题
求证：不交于同一个点的四条直线两两相交，则这四条直线共面．
答案
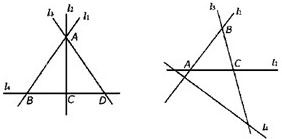
（1）若三直线l1、l2、l3交于一点A（如图），
则由点A与l4确定一个平面α
A∈α，B∈α，AB?α，l1?α，
同理可得l2?α．、l3?α，
∴l1、l2、l3、l4四点共面．
（2）若四直线无三线共点，设两直线交于一点，
如l1∩l2=A．，则l1、l2确定一个面α，则B∈α，C∈α?l3?α．
同理l4?α?四线共面．
搜题请搜索小程序“爱下问搜题”