问题
解答题
设a,b为异面直线,EF为a,b的公垂线,α为过EF的中点且与a,b平行的平面,M为a上任一点,N为b上任一点,求证线段MN被平面α二等分.
答案
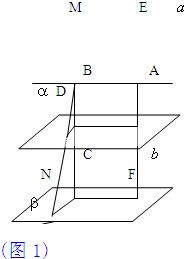
证明:过直线b作平面β∥α(如图1).
过直线a及公垂线EF作一平面,在此平面内作MC∥EF,且与平面α,β分别交于B、C两点,
设EF、MN分别与平面α交于点A、D,
∵点A是EF的中点,
又ME∥BA∥CF,
∴点B是MC的中点,
又∵DB∥NC,
∴D是MN的中点.
