f′(x)=

1

x

-a-

1-a

x2

=-

ax2-x+1-a

x2

=-

[ax+(a-1)](x-1)

x2

（x＞0），

令g（x）=ax²-x+1-a，

①当a=0时，g（x）=-x+1，当x∈（0，1）时，g（x）＞0，f′（x）＜0，函数f（x）单调递减；

当x∈（1，+∞）时，g（x）＜0，f′（x）＞0，函数f（x）单调递增；

②当0＜a＜

1

2

时，由f′（x）=0，x₁=1，x₂=

1

a

-1．此时

1

a

-1＞1＞0，

列表如下：

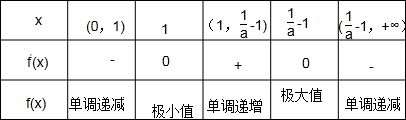
由表格可知：函数f（x）在区间（0，1）和(

1

a

-1，+∞)上单调递减，在区间(1，

1

a

-1)上单调递增；

③当a=

1

2

时，x₁=x₂，此时f′（x）＜0，函数f（x）在（0，+∞）单调递减；

④当a＜0时，由于

1

a

-1＜0，则函数f（x）在（0，1）上单调递减；在（1，+∞）上单调递增．

综上：当a≤0时，函数f（x）在（0，1）上单调递减；在（1，+∞）上单调递增．

当a=

1

2

时，函数f（x）在（0，+∞）上单调递减．

当0＜a＜

1

2

时，函数f（x）在区间（0，1）和(

1

a

-1，+∞)上单调递减，在区间(1，

1

a

-1)上单调递增．