问题
解答题
四面体ABCD中,E、G分别为BC、AB的中点,F在CD上,H在AD上,且有DF:FC=2:3.DH:HA=2:3.
(1)证明:点G、E、F、H四点共面;
(2)证明:EF、GH、BD交于一点.
答案
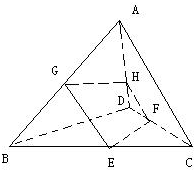
证明:(1)∵E、G分别为BC、AB的中点,∴EG∥AC
又∵DF:FC=2:3.DH:HA=2:3,∴FH∥AC.
∴EG∥FH
所以,E、F、G、H四点共面.
(2)由(1)可知,EG∥FH,且EG≠FH,即EF,GH是梯形的两腰,
所以它们的延长线必相交于一点P
∵BD是EF和GH分别所在平面BCD和平面ABD的交线,而点P是上述两平面的公共点,
∴由公理3知P∈BD.
所以,三条直线EF、GH、BD交于一点.
