（1）因f/(x)=

a(x2+b)-ax(2x)

(x2+b)2

，

而函数f(x)=

ax

x2+b

在x=1处取得极值2，

所以

f/(1)=0 f(1)=2

⇒

a(1+b)-2a=0 a 1+b =2

⇒

a=4 b=1

所以f(x)=

4x

1+x2

；

（2）由（1）知f/(x)=

4(x2+1)-8x2

(x2+1)2

=

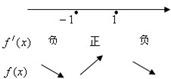
-4(x-1)(x+1)

(1+x2)2

，

如图，f（x）的单调增区间是[-1，1]，

所以，

m≥-1 2m+1≤1 m＜2m+1

⇒-1＜m≤0，

所以当m∈（-1，0]时，函数f（x）在区间（m，2m+1）上单调递增．

（3）由条件知，过f（x）的图形上一点P的切线l的斜率k为：k=f/(x0)=

4(1-x02)

(1+x02)2

=4×

-1-x02+2

(1+x02)2

=4[

2

(1+x02)2

-

1

1+x02

]

令t=

1

1+x02

，则t∈（0，1]，此时，k=8(t2-

1

2

t)=8(t-

1

4

)2-

1

2

根据二次函数k=8(t-

1

4

)2-

1

2

的图象性质知：

当t=

1

4

时，k_min=-

1

2

，当t=1时，k_max=4

所以，直线l的斜率k的取值范围是[-

1

2

 ， 4 ]．