问题
填空题
设函数f(x)=x3+3bx2+3cx存在两个极值点x1,x2,且x1∈[-1,0],x2∈[1,2]则b2+c2的范围为______.
答案
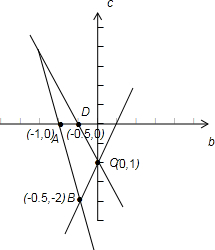
f′(x)=3x2+6bx+3c,
由题意知方程f′(x)=0有两个根x1,x2,
且x1∈[-1,0],x2∈[1,2]则有f′(-1)≥0,f′(0)≤0,f′(1)≤0,f′(2)≥0.
即满足下列条件
2b-c-1≤0,c≤0,2b+c+1≤0且4b+c+4≥0.
故有图中四边形ABCD即是满足这些条件的点(b,c)的区域.
则b2+c2表示点(b,c)与原点距离的平方.
根据两点之间的距离公式与点到直线的距离公式可得:b2+c2的范围为[
,1 5
].17 4
故答案为[
,1 5
].17 4
