解：满足a²+b²≤34的条件中的点（a，b），位于半径为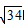的圆内．

函数f（x）=的导数f′（x）=2ax?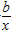+1，要使函数在区间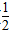（ ，1）上不单调，则说明f'（x）=0的根在区间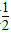（ ，1），

即f′（1）f′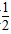（）＜0，所以（2a-b+1）（a-2b+1）＜0，

即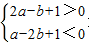   或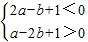且a＞0，0＜b≤3，

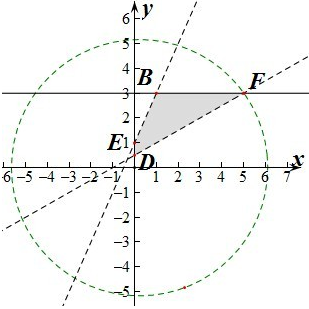
作出不等式组对应的可行域如图阴影部分：

令b=3，解的x_B=1，x_F=5，即B（1，3），C（5，3）．

同理可知D（0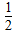，），E（0，1），

所以阴影部分的面积为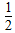 ×5×（3?）? ×1×（3?1）=．

圆的面积为π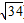（ ）²=34π．

所以由几何概型公式可得使函数f（x）=ax²-blnx+x（a＞0，0＜b≤3）

在区间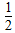（，1）上不单调的概率为P=．

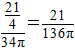故选A．