已知函数,f(x)=
(1)若方程f(x)-m=0有两个不相等的实数根,求实数m的取值范围; (2)若直线L是函数y=f(x)的图象在点(2,f(2))处的切线,且直线L与函数Y=G(X)的图象相切于点P(x0,y0),x0∈[e-1,e],求实数b的取值范围. |
(1)x>0时,f(x)=(x2-2ax)ex,
∴f'(x)=(2x-2a)ex+(x2-2ax)ex=[x2+2(1-a)x-2a]ex,
由已知,f′(
)=0,∴[2+22
(1-a)-2a]e2
=0,2
∴2+2
-2a-22
a=0,∴a=1,2
∴x>0时,f(x)=(x2-2x)ex,
∴f'(x)=(2x-2)ex+(x2-2x)ex=(x2-2)ex.
令f'(x)=0得x=
(x=-2
舍去)2
当x>0时,
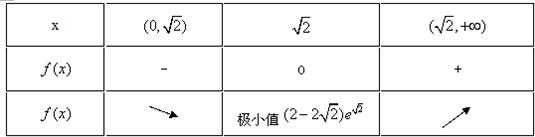
∴当 x∈(0,
)时,f(x)单调递减,当 x∈(2
,+∞),f(x)单调递增,2
∴x>0时,f(x)∈((2-2
)e2
,+∞)2
要使方程f(x)-m=0有两不相等的实数根,即函数y=f(x)的图象与直线y=m有两个不同的交点.
①当b>0时,m=0或 m=(2-2
)e2
;2
②当b=0时,m∈((2-2
)e2
,0);2
③当b<0时,m∈((2-2
)e2
,+∞)2
(2)x>0时,f(x)=(x2-2x)ex,f'(x)=(x2-2)ex,∴f(2)=0,f'(2)=2e2.
函数f(x)的图象在点(2,f(2))处的切线l的方程为:y=2e2(x-2),
∵直线l与函数g(x)的图象相切于点P(x0,y0),x0∈[e-1,e],∴y0=clnx0+b,g′(x)=c x
∴切线l的斜率为 g′(x0)=c x0
∴切线l的方程为:y-y0=
(x-x0),即y=c x0
x-c+b+clnx0,c x0
∴
,∴
=2e2c x0 -c+b+clnx0=-4e2 c=2e2x0 b=c-clnx0-4e2
∴b=2e2(x0-x0lnx0-2),其中x0∈[e-1,e]
记h(x0)=2e2(x0-x0lnx0-2),其中x0∈[e-1,e],h'(x0)=-2e2lnx0,
令h'(x0)=0,得x0=1.
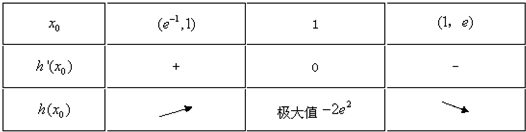
又h(e)=-4e2,h(e-1)=4e-4e2>-4e2.
∵x0∈[e-1,e],∴h(x0)∈[-4e2,-2e2],
∴实数b的取值范围为:{b|-4e2≤b≤-2e2}.
