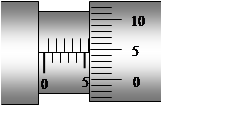
已知函数f(x)=
(I)证明:-27<c<5; (II)若存在实数c,使函数f(x)在区间[a,a+2]上单调递减,求a的取值范围. |
(I)因为函数f(x)=
x4+x3-1 4
x2+cx有三个极值点,9 2
所以f'(x)=x3+3x2-9x+c=0有三个互异的实根.
设g(x)=x3+3x2-9x+c,则g'(x)=3x2+6x-9=3(x+3)(x-1),
当x<-3时,g'(x)>0,g(x)在(-∞,-3)上为增函数;
当-3<x<1时,g'(x)<0,g(x)在(-3,1)上为减函数;
当x>1时,g'(x)>0,g(x)在(1,+∞)上为增函数;
所以函数g(x)在x=-3时取极大值,在x=1时取极小值.
当g(-3)≤0或g(1)≥0时,g(x)=0最多只有两个不同实根.
因为g(x)=0有三个不同实根,所以g(-3)>0且g(1)<0.
即-27+27+27+c>0,且1+3-9+c<0,
解得c>-27,且c<5,故-27<c<5.
(II)由(I)的证明可知,当-27<c<5时,f(x)有三个极值点.
不妨设为x1,x2,x3(x1<x2<x3),则f'(x)=(x-x1)(x-x2)(x-x3).
所以f(x)的单调递减区间是(-∞,x1],[x2,x3]
若f(x)在区间[a,a+2]上单调递减,
则[a,a+2]⊂(-∞,x1],或[a,a+2]⊂[x2,x3],
若[a,a+2]⊂(-∞,x1],则a+2≤x1.由(I)知,x1<-3,于是a<-5.
若[a,a+2]⊂[x2,x3],则a≥x2且a+2≤x3.由(I)知,-3<x2<1.
又f'(x)=x3+3x2-9x+c,当c=-27时,f'(x)=(x-3)(x+3)2;
当c=5时,f'(x)=(x+5)(x-1)2.
因此,当-27<c<5时,1<x3<3.所以a>-3,且a+2≤3.
即-3<a<1.故a<-5,或-3<a<1.反之,当a<-5,或-3<a<1时,
总可找到c∈(-27,5),使函数f(x)在区间[a,a+2]上单调递减.
综上所述,a的取值范围是(-∞,-5)∪(-3,1).

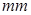 ; 螺旋测微器的读数
; 螺旋测微器的读数