问题
问答题
设函数f(x)=2x3-3(a-1)x2+1,分别对a=1和a>1两种情况求 f(x)的单调区间和极值.
答案
参考答案:
解析:本题考查的知识点是对不同的。值判定函数单调性及求其极值.
解 因为f’(x)=6x2-6x(a-1).
(1)当a=1时
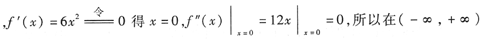
内f(x)单调递增,且无极值.
(2)当a>1时,
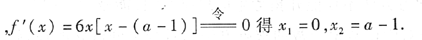
因为f”(x)=6[2x-(a-1)],f”(0)<0,所以f(0)=1为极大值;f”(a-1)>0,所以f(a-1)=1-(a-1)3为极小值.
本题也可列表进行解答:
| x | (-∞,0) | 0 | (0,a-1) | a-1 | (a-1,+∞) |
| f’(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
