问题
解答题
某校初三学生开展踢毽子活动，每班派5名学生参加，按团体总分排列名次，在规定时间内每人踢100个以上（含100）为优秀．下表是甲班和乙班成绩最好的5名学生的比赛成绩．
请你回答下列问题： （1）甲乙两班的优秀率分别为 、 ； （2）计算两班比赛数据的方差； （3）根据以上三条信息，你认为应该把团体第一名的奖状给哪一个班？简述理由． |
答案
(1)60%，40%；（2）S甲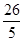2=
，S乙2=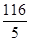
；（3）甲班，理由见解析.
题目分析：（1）根据甲班和乙班每人踢100个以上（含100）的人数，除以总人数，即可求出甲乙两班的优秀率；
（2）根据平均数的计算公式先求出甲和乙的平均数，再根据方差公式进行计算即可；
（3）分别从甲和乙的优秀率、中位数、方差方面进行比较，即可得出答案．
试题解析：（1）甲班的优秀率为：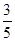
×100%=60%，
乙班的优秀率为：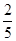
×100%=40%；
(2)甲的平均数为：（100+98+102+97+103）÷5=100（分），
S甲2=[（100-100）2+（98-100）2+（102-100）2+（97-100）2+（103-100）2]÷5= ；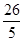
乙的平均数为：（99+100+95+109+97）÷5=100（分），
S乙2=[（99-100）2+（100-100）2+（95-100）2+（109-100）2+（97-100）2]÷5= ；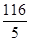
（3）应该把团体第一名的奖状给甲班，理由如下：
因为甲班的优秀率比乙班高；甲班的中位数比乙班高；甲班的方差比乙班低，比较稳定，综合评定甲班比较好．
考点: 1.方差；2.平均数；3.统计表.