问题
问答题
设A为n阶实对称矩阵,秩(A)=n,Aij是A=(aij)n×m中元素aij的代数余子式(i,j=1,2,…,n),二次型
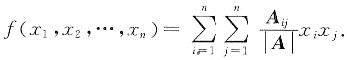
(1) 记X=(x1,x2,…,xn)。,把f(x1,x2,…,xn)写成矩阵形式,并证明二次型f(X)的矩阵为A-1;
(2) 二次型g(X)=XTAX与f(X)的规范形是否相同说明理由.
答案
参考答案:(1) 由题设,
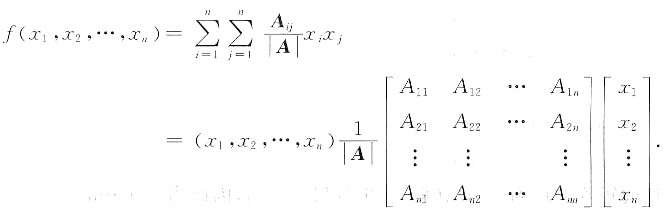
已知A为n阶实对称矩阵,从而上式中矩阵可换成共转置.即

已知r(A)=n,从而|A|≠0,A可逆,且
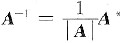 ,则由(1)式知
,则由(1)式知
f(x1,x2,…,xn)=XTA-1X且(A-1)T=(AT)-1=A-1,
故f(x1,x2,…,xn)=XTA-1X是f(X)的矩阵表示,且相应矩阵为A-1,证毕.
(2) 由于(A-1)TAA-1=(AT)-1E=A-1,则A-1与A合同,于是g(X)=XTAX与f(X)有相同规范形.
解析:[考点提示] 二次型、矩阵的合同.
[评注] 关于(2)的证明中A-1与A合同的结论,也可通过以下方法得到:对二次型g(X)=XTAX作可逆线性变换X=A-1Y,其中Y=(y1,y2,…,yn)T,则
g(X)=XTAX=(A-1Y)TA(A-1Y)=YT(A-1)TAA-1Y
=YT(AT)-1AA-1Y=YTA-1Y,
则A与A-1合同.
