问题
问答题
假设由自动生产线加工的某种零件的内径X(单位:毫米)服从正态分布N(μ,1),内径小于10或大于12的为不合格品,其余为合格品,销售每件合格品获利,销售每件不合格品亏损.已知销售利润T(单位:元)与销售零件的内径X有如下关系:
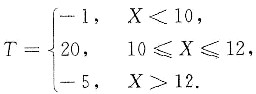
问平均内径μ取何值时,销售一个零件的平均利润最大
答案
参考答案:因为X~N(u,1),所以
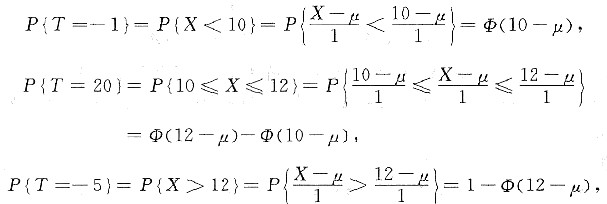
于是销售一个零件的平均利润
E(T)=-1×P{T=-1)+20×P{T=20}+(-5)×P{T=-5)
=-φ(10-μ)+20[φ(12-μ)-φ(10-μ)]-5[1-φ(12-μ)]
=25φ(12-μ)-21φ(10-μ)-5.
令
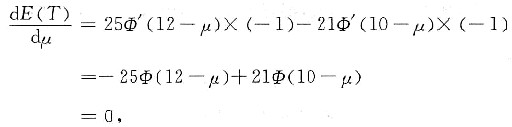
得
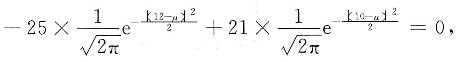
即
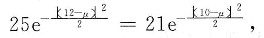
两边取对数得
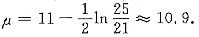
所以μ=10.9毫米时,销售一个零件的平均利润最大.
[评注] 这里μ是确定性的参变量,而X、T是随机变量.本题将随机变量的数学期望问题与极值问题综合了起来,解决问题的关键是用标准正态分布函数φ(x)表示离散型随机变量T的概率分布,且此问题的最大值为:
E(T)|μ=10.9=25φ(12-10.9)-21φ(10-10.9)-5
=25×0.8643=21×(1-0.8159)=5
≈12.74(元).
解析:[考点提示] 平均利润就是销售利润丁的数学期望E(T),它是参数u的函数,问题即为求E(T)达到最大时参数u的值.
