问题
问答题
设银行存款的年利率r=0.05,并依年复利计算.某基金会希望通过存款A万元实现第一年取出19万元,第二年取出28万元,…,第n年取出(10+9n)万元,并能按此规律一直取下去,问A至少为多少万元
答案
参考答案:此问题可假设每次取出的钱在当年存上,则n年后A万元变为A(1+0.05)n万元;取钱再存上后钱的数量为
19(1+0.05)n-1+28(1+0.05)n-2+…+(10+9n)·1.
依题意当n→∞时,
A(1+0.05)n≥19(1+0.05)n-1+28(1+0.05)n-2+…+(10+9n)·1,
即
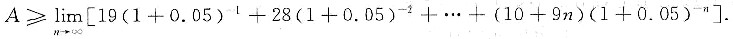
又
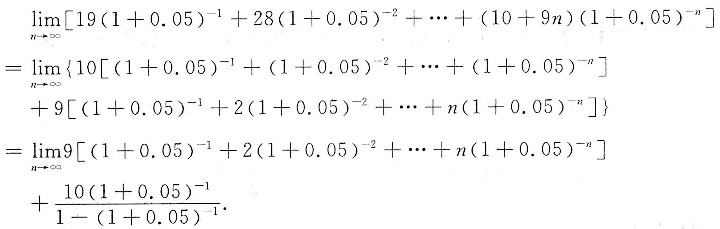
令Sn=(1+0.05)-1+2(1+0.05)-2+…+n(1+0.05)-n,则
(1+0.05)-1Sn=(1+0.05)-2+2(1+0.05)-3+…+n(1+0.05)-n-1.上述两式相减得
[1-(1+0.05)-1Sn=(1+0.05)-1
于是
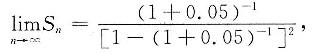
则有
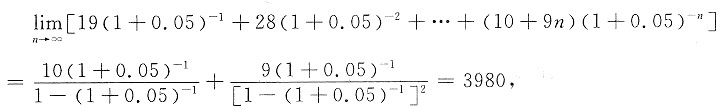
故A≥3980.所以A至少为3980万元,才可以一直取下去.
解析:[考点提示] 数列与极限在经济学中的应用.
