问题
问答题
设曲线方程为y=e-x(x≥0)．
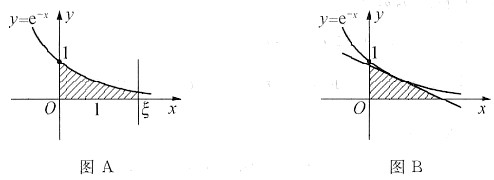
(1) 把曲线y=e-x(x≥0)，x轴，y轴和直线x=ξ(ξ＞0)所围成平面图形绕x轴旋转一周，得一旋转体，求此旋转体的体积V(ξ)；求满足
的a．
(2) 在此曲线上找一点，使过该点的切线与两个坐标轴所夹平面图形的面积最大，并求出该面积．
答案
参考答案：(1) 如图A，旋转体体积
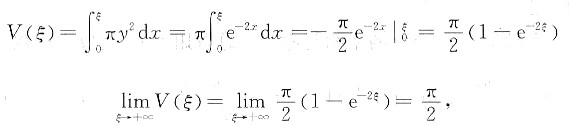
由
得
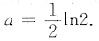
(2) 如图B．设切点为(a，e-a)，因y’=(e-x)’=-e-x，所以切线方程为
y-e-a=-e-a(x-a)，
令x=0，得y=(1+a)e-a，令y=0，得x=1+a，于是切线与坐标轴所夹面积
令S’=0，得a1=1，a2=-1，其中a2=-1应舍去．
当a＜1时，
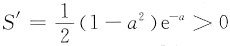；当a＞1时，
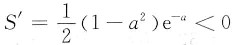，故当a=1时，面积最大，所求切点为(1，e-1)，最大面积
解析：[考点提示] (1)先利用定积分求旋转体体积的公式求V(ξ)，并求出极限[*]，然后解出a．(2)是导数在求最值问题中的应用，首先建立切线与坐标轴所夹图形的面积关于切点的目标函数，然后运用导数方法求出极限值点和极值．
[评注] 本题综合考查了微分学与积分学的多个知识点：切线问题，面积与体积问题，极限与极值问题，但涉及的每个知识点都是基本内容，这是考研综合题型的典型特点．