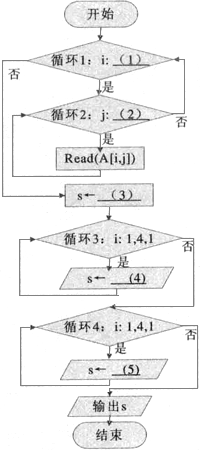
问题
解答题
| (1)请用“>”、“<”、“=”填空: ①32+22______2×3×2 ②52+52______2×5×5 ③(
④(-6)2+32______2×(-6)×3 ⑤(-2)2+(-2)2______2×(-2)×(-2) (2)观察以上各式,请猜想a2+b2与2ab的大小; (3)你能借助于完全平方公式证明你的猜想吗?试试看! |
答案
(1)①32+22=13,2×3×2=12,
故32+22>2×3×2,
②52+52=20,2×5×5=20,
故52+52=2×5×5,
③(
)2+(3
)2=5=2
,2×25
×3
=2
,24
故(
)2+(3
)2>2×2
×3
,2
④(-6)2+32=45,2×(-6)×3=-36,
故(-6)2+32>2×(-6)×3,
⑤(-2)2+(-2)2=8,2×(-2)×(-2)=8,
故(-2)2+(-2)2=2×(-2)×(-2);
(2)a2+b2≥2ab;
(3)∵(a-b)2≥0,
∴a2-2ab+b2≥0,
即a2+b2≥2ab.

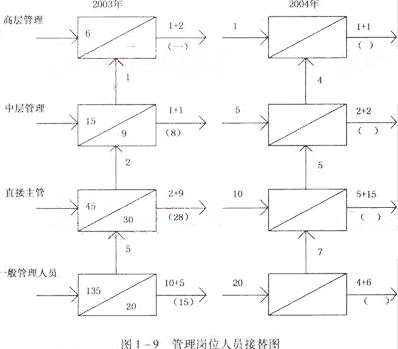
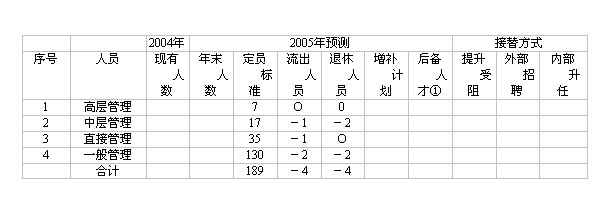 注:系指本层次待提升者人数问题:
注:系指本层次待提升者人数问题: