问题
问答题
一辆长途客车正在以v=20m/s的速度匀速行驶．突然，司机看见车的正前方x=33m处有一只狗，如图（甲）所示，司机立即采取制动措施．若从司机看见狗开始计时（t=0），长途客车的速度-时间图象如图（乙）所示，g取l0m/s2．
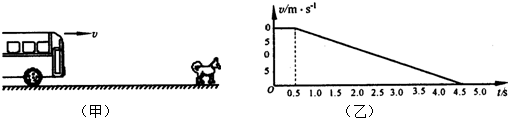
（1）求长途客车从司机发现狗至停止运动的这段时间内前进的距离．
（2）求长途客车与地面间的动摩擦因数．
（3）若狗正以v′=4m/s的速度与长途客车同向奔跑，问狗能否摆脱被撞的噩运？
答案
（1）在v-t图象中，面积表示位移，所以客车司机从发现狗至停止运动的这段时间内前进：
s=20×0.5+20×4÷2=50m
（2）客车减速运动的加速度为：a=
=-5m/s，△v t
由于客车制动后在摩擦力做用下做匀减速直线运动，由牛顿第二定律有：
-μmg=ma
μ=-
=0.5a g
（3）客车减速的加速度为：a=
=-5m/s2△v t
客车由v0=20m/s，减速到v1=4m/s，所需要的时间为：t=
=3.2s△v a
司机从看到狗到客车减速为v1=4m/s所前进的位移：X1=v0t′+
=48.4mv12-v02 2a
这段时间内狗前进的位移为：X2=v'（t'+t1）=4×（0.5+3.2）=14.8m
因为：X1＞X+X2
所以，狗将被客车撞上．
答：（1）长途客车从司机发现狗至停止运动的这段时间内前进的距离为50m．
（2）长途客车与地面间的动摩擦因数0.5
（3）狗将被客车撞上．