问题
问答题
从地面上以初速度v0竖直向上抛出一质量为m的球,若运动过程中受到的空气阻力与其速率成正比关系,球运动的速率随时间变化规律如图所示,t1时刻到达最高点,再落回地面,落地时速率为v1,且落地前球已经做匀速运动.求:
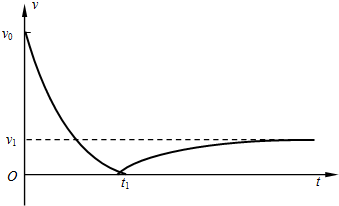
(1)球从抛出到落地过程中克服空气阻力所做的功;
(2)球抛出瞬间的加速度大小;
(3)球上升的最大高度H.
答案
(1)由动能定理得
Wf=
mv12-1 2
mv021 2
克服空气阻力做功
W=-Wf=
mv02-1 2
mv121 2
(2)空气阻力f=kv
落地前匀速运动,则mg-kv1=0
刚抛出时加速度大小为a0,则
mg+kv0=ma0
解得a0=(1+
)gv0 v1
(3)上升时加速度为a,-(mg+kv)=ma
a=-g-
vk m
取极短△t时间,速度变化△v,有:
△v=a△t=-g△t-
v△tk m
又v△t=△h
上升全程∑△v=0-v0=-g∑△t-
∑△hk m
则v0=gt1+
Hk m
H=(v0-gt1)v1 g
答:(1)球从抛出到落地过程中克服空气阻力所做的功为
mv02-1 2
mv12;1 2
(2)球抛出瞬间的加速度大小为(1+
)g;v0 v1
(3)球上升的最大高度H为
.(v0-gt1)v1 g
