已知抛物线y=3ax2+2bx+c，
（1）若a=b=1，c=﹣1，求该抛物线与x轴公共点的坐标；
（2）若a=b=1，且当﹣1＜x＜1时，抛物线与x轴有且只有一个公共点，求c的取值范围；
（3）若a+b+c=0，且x1=0时，对应的y1＞0；x2=1时，对应的y2＞0，试判断当0＜x＜1时，抛物线与x轴是否有公共点？若有，请证明你的结论；若没有，阐述理由．
解：（1）当a=b=1，c=﹣1时，抛物线为y=3x2+2x﹣1，
方程3x2+2x﹣1=0的两个根为x1=﹣1，
．
∴该抛物线与x轴公共点的坐标是（﹣1，0）和（
，0）；
（2）当a=b=1时，抛物线为y=3x2+2x+c，且与x轴有公共点．
对于方程3x2+2x+c=0，判别式△=4﹣12c≥0，有c≤
．
①当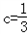
时，由方程3x2+2x+
=0，解得x1=x2=﹣
．
此时抛物线为y=3x2+2x+
与x轴只有一个公共点（﹣
，0）；
②当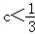
时，x1=﹣1时，y1=3﹣2+c=1+c；x2=1时，y2=3+2+c=5+c．
由已知﹣1＜x＜1时，该抛物线与x轴有且只有一个公共点，考虑其对称轴为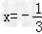
，
应有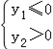
即
，
解得﹣5＜c≤﹣1．
综上，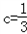
或﹣5＜c≤﹣1．
（3）对于二次函数y=3ax2+2bx+c，
由已知x1=0时，y1=c＞0；x2=1时，y2=3a+2b+c＞0，
又∵a+b+c=0，
∴3a+2b+c=（a+b+c）+2a+b=2a+b．
∴2a+b＞0．
∵b=﹣a﹣c，
∴2a﹣a﹣c＞0，即a﹣c＞0．
∴a＞c＞0．
∵关于x的一元二次方程3ax2+2bx+c=0的判别式△=4b2﹣12ac=4（a+c）2﹣12ac=4[（a﹣c）2+ac]＞0，
∴抛物线y=3ax2+2bx+c与x轴有两个公共点，顶点在x轴下方．
又该抛物线的对称轴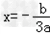
，由a+b+c=0，c＞0，2a+b＞0，得﹣2a＜b＜﹣a，
∴
．
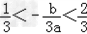又由已知x1=0时，y1＞0；x2=1时，y2＞0，
观察图象，可知在0＜x＜1范围内，该抛物线与x轴有两个公共点．
