问题
问答题
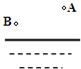
如图所示,一人从A处出发到河岸边提水送到B处,请画出他行走的最短路程,并简述理由.
答案
如图1所示,做A关于河岸的对称点A′,连接A′B与河岸相交于点O,则行走的最短路程为由A到O再到B.
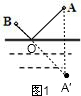
若在河岸上任意取一点O′,连接AO′、O′B,如图2所示.
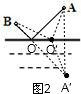
因为A、A′关于河岸对称,所以河岸是AA′的垂直平分线,所以O′A′=O′A,OA′=OA.
则OA+OB=OA′+OB=A′B
O′A+O′B=O′A′+O′B>A′B(三角形的两边之和大于第三边)
所以O′A+O′B>OA+OB
因此,图1所示的走法路程最短.
