问题
填空题
已知四面体ABCD中，AB=AD=6，AC=4，CD=2
|
答案
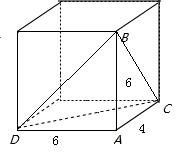
由题意可知几何体是长方体的一部分，如图，
长方体的对角线的长为l=
=AD2+AC2+AB2
=62+42+62
，就是外接球的直径，88
所以外接球的直径为：
，所以球的表面积为：4π（88
）2=88π．88 2
故答案为：88π．
搜题请搜索小程序“爱下问搜题”
已知四面体ABCD中，AB=AD=6，AC=4，CD=2
|
由题意可知几何体是长方体的一部分，如图，
长方体的对角线的长为l=
=AD2+AC2+AB2
=62+42+62
，就是外接球的直径，88
所以外接球的直径为：
，所以球的表面积为：4π（88
）2=88π．88 2
故答案为：88π．