问题
解答题
已知函数f(x)=
(I)求f(x)的单调区间; (II)若g(x)=-
|
答案
(I)∵f(x)=
x2-lnx的定义域为(0,+∞),1 2
又f(x)可得:f′(x)=x-
=1 x x2-1 x
令f'(x)=0,则x=1
当x变化时,f'(x),f(x)的变化情况如下表:
| x | (0,1) | 1 | (1,+∞) |
| f'(x) | - | 0 | + |
| f(x) | 递减 | 极小值 | 递增 |
(II)令h(x)=f(x)-g(x)=
x3-2 3
x2-lnx1 2
则h′(x)=2x2-x-
=1 x
=2x3-x2-1 x (x-1)(2x2+x+1) x
∵x>1
∴h'(x)>0
∴h(x)在(1,+∞)上单调递增
又h(1)=
>01 6 ∴f(x)>g(x)
当x>1时,f(x)的图象恒在g(x)图象的上方.

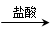 测得生成气体的体积Vml(已折算成标准状况);
测得生成气体的体积Vml(已折算成标准状况); 测得剩余固体的质量a克;
测得剩余固体的质量a克; 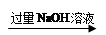 测得沉淀的质量b克。
测得沉淀的质量b克。