问题
填空题
球O上两点A、B间的球面距离为
|
答案
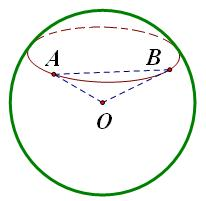
∵△AOB中，OA=OB，且有一个内角为
，π 3
∴△OAB是等边三角形，∠AOB=π 3
设球半径为R，则A、B间的球面距离为
L=θR=
R=π 3
?R=π 2 3 2
∴此球的体积是V=
πR3=4 3
π(4 3
)3=3 2 9π 2
故答案为：9π 2
搜题请搜索小程序“爱下问搜题”
球O上两点A、B间的球面距离为
|
∵△AOB中，OA=OB，且有一个内角为
，π 3
∴△OAB是等边三角形，∠AOB=π 3
设球半径为R，则A、B间的球面距离为
L=θR=
R=π 3
?R=π 2 3 2
∴此球的体积是V=
πR3=4 3
π(4 3
)3=3 2 9π 2
故答案为：9π 2