阅读短文,回答问题:
干簧管
干簧管是一种利用磁场信号来控制的线路开关器件,也叫磁控开关。常用的干簧管有单触点和双触点两种。
如图为单触点干簧管的结构示意图。其外壳是一根密封的玻璃管,管中装有两个磁性材料制成的弹性簧片电板,还灌有一种惰性气体。平时,玻璃管中的两个磁簧片触点部位是分开的(如图甲)。当有磁性物质靠近玻璃管时,在合适的磁场的作用下,管内的两个簧片的触点部位被磁化成为异名磁极就会互相吸引接触,簧片就会吸合在一起,使结点所接的电路连通(如图乙)。外磁力消失后,两个簧片由于本身的弹性而分开,线路就断开。

干簧管中的磁性材料是指铁、钴、镍等能被磁铁吸引的材料,它分为软磁性材料和硬磁性材料两种。软磁性材料是指既容易被磁化而获得磁性又很容易失去磁性的物质。硬磁性材料是指不容易被磁化而获得磁性,但一旦获得磁性又很不容易失去的物质。磁体周围的磁性材料被磁化后的极性与放置在该处的小磁针的极性相似,如我们拿一根铁棒的一端靠近或接触磁铁的N极时,这一端就会被磁化成S极,它的另一端则会被磁化成N极。
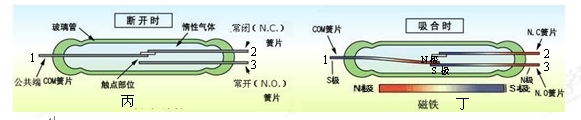
双触点干簧管类似于单刀双掷开关,它的工作原理是:没有磁场时,簧片1与簧片2接通(如图丙),当有外界磁力时,簧片1与簧片2的连接断开,簧片1与簧片3触点部位接通(如图丁),其中簧片1是公共端,簧片2是常闭接点,簧片3是常开接点。簧片中有一片是用只导电不导磁的材料做成。
干簧管外绕上能产生磁场的线圈就成了干簧继电器,当线圈通电后,管中磁性材料制
成的簧片的自由端分别被磁化成N极和S极而相互吸引,因而接通被控电路。线圈断电后,干簧片在本身的弹力作用下分开,将线路切断。
(1)单触点干簧管中的磁簧片是用_______(选填“软”或“硬”)磁性材料制成的。
(2)单触点干簧管在___________(选填“断开”或“闭合”)时,磁簧片具有弹性势能。
(3)双触点干簧管的1、2、3三个簧片的对应制作材料可能是________
A.铁、铁、铜 B.铁、铜、铁 C.铜、铁、铜 D.铁、钴、铁
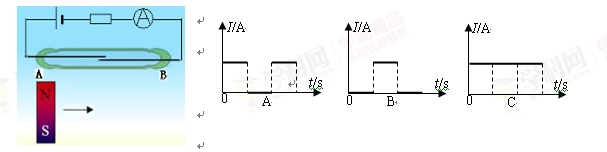
(4)当条形磁铁按左图所示的方式从A移动到B,下列能反映电路中的电流随时间变化的图象是______。
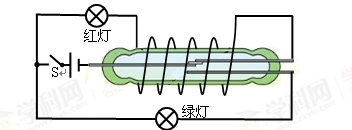
(5)如图为一运用干簧继电器的电路,当开关S闭合后,它的工作特点是________
A.红灯、绿灯交替发光
B.红灯长亮,绿灯亮、灭交替
C.绿灯长亮,红灯亮、灭交替
D.红灯长亮,绿灯不亮