问题
问答题
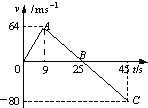
一空间探测器从某一星球表面竖直升空,假设探测器质量恒为1500kg,发动机推动力F为恒力,若探测器升空过程中发动机突然关闭,其速度随时间的变化情况如图所示,图线上A、B、C三点对应的时刻分别为9s、25s和45s.已知该星球表面没有空气.试求:
(1)求探测器在该星球表面达到的最大高度H;
(2)求该星球表面的重力加速度;
(3)求发动机的推动力F大小.
答案
(1)v-t图象包围的面积表示位移.由图象可知,在25秒末探测器达到最大高度
H=
=800m64×25 2
(2)AB段是探测器到达最高点后做自由落体运动.所以AB直线的加速度为该星球的重力加速度,其斜率表示加速度.
g=
=4m/s264 25-9
(3)0A段是探测器竖直上升阶段.斜率表示上升的加速度,a1=
m/s264 9
根据牛顿第二定律:F-mg=ma1
所以F=m(a1+g)=1500×(
+4)N=1.67×104N.64 9
答:(1)探测器在该星球表面达到的最大高度H为800m;
(2)该星球表面的重力加速度为4m/s2;
(3)发动机的推动力F大小为1.67×104N.
