问题
解答题
已知函数f(x)=(x2-2ax)e
(Ⅰ)若a=1,求曲线y=f(x)在点(0,f(0))处的切线方程; (II)求函数f(x)的单调区间. |
答案
(I)当a=1时,f(x)=(x2-2x)ex,f′(x)=(2x-2)ex+(x2-2x)ex=(x2-2)ex,
当x=0时,f(0)=0,f′(0)=-2,
所以曲线y=f(x)在点(0,f(0))处的切线方程y-0=-2(x-0),即y=-2x.
(II)f(x)的定义域为R,则f′(x)=(2x-2a)e
+(x2-2ax)ex a
•x a
=(1 a
x2-2a)e1 a
,x a
(1)当a>0时,由(
x2-2a)e1 a
>0,得x2-2a2>0,解得x<-x a
a或x>2
a,2
由(
x2-2a)e1 a
<0,得x2-2a2<0,解得-x a
a<x<2
a,2
故f(x)的增区间为(-∞,-
a),(2
a,+∞),减区间为(-2
a,2
a);2
(2)当a<0时,由(
x2-2a)e1 a
>0,得x2-2a2<0,解得x a
a<x<-2
a,2
由(
x2-2a)e1 a
<0,得x2-2a2>0,解得x<x a
a或x>-2
a,2
故f(x)的增区间为(
a,-2
a),减区间为(-∞,2
a),(-2
a,+∞).2

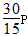 →
→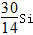 +x
+x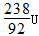 →
→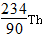 +x
+x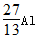 +
+ →
→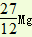
 +
+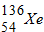 →
→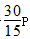 +x
+x