问题
填空题
已知三棱锥S-ABC的所有顶点都在以O为球心的球面上,△ABC是边长为1的正三角形,SC为球O的直径,若三棱锥S-ABC的体积为
|
答案
根据题意作出图形:
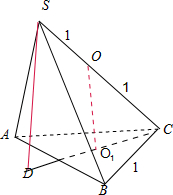
设球心为O,球的半径r.过ABC三点的小圆的圆心为O1,则OO1⊥平面ABC,
延长CO1交球于点D,则SD⊥平面ABC.
∵CO1=
×2 3
=3 2
,3 3
∴OO1=
=r2-(
)23 3
,r2- 1 3
∴高SD=2OO1=2
,r2- 1 3
∵△ABC是边长为1的正三角形,
∴S△ABC=
,3 4
∴V三棱锥S-ABC=
×1 3
×23 4
=r2- 1 3
,2 6
∴r=1.则球O的表面积为 4π
故答案为:4π.
