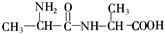| 已知函数f(x)=x3-3ax2+2ax+1(a∈R). (I)当a=-
(Ⅱ) 当a>0时,设函数g(x)=f(x)+3-2ax,若x∈[1,2]时,g(x)>0恒成立,求a的取值范围. |
(I)当a=-
时,函数为f(x)=x3+3 8
x2-9 8
x+1,3 4
则f/(x)=3x2+
x-9 4
<0,解得当-1<x<3 4
时,1 4
所以函数f(x)的单调递减区间为(-1,
). (3分)1 4
(Ⅱ) g(x)=x3-3ax2+4,则g′(x)=3x2-6ax=3x(x-2a),
令g′(x)=0,解得x=0或x=2a
(1)若0<a≤
,在区间x∈[1,2]上时,g′(x)>0,即g(x)在区间[1,2]上单调递增1 2
所以有g(1)>0,解得a<
,故0<a≤5 3 1 2
(2)若
<a<1,当x∈[1,2a]时,函数g(x)单调递减,1 2
当x∈[2a,2]时,函数g(x)单调递增,所以有g(2a)>0,解得a<1,故
<a<1(7分)1 2
(3)若a≥1,当x∈[1,2]时,g′(x)<0,即g(x)在区间[1,2]上单调递减,
所以有g(2)>0,解得a<1,舍去
综上所述,当0<a<1时,x∈[1,2],g(x)>0恒成立. (10分)

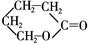
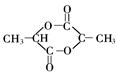 ⑦
⑦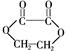 ⑧
⑧