问题
解答题
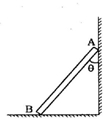
已知函数f(x)=
(1)若函数y=f(x)的导函数是偶函数,求a的值; (2)若y=f(x)的图象在点(1,f(1))处的切线方程为x+y-3=0,求f(x)在区间[-2,4]上的最大值; (3)当a≠0时,若f(x)在区间(-1,1)上不单调,求a的取值范围. |
答案
(1)由题意得,f'(x)=x2-2ax+a2-1,
∵f'(x)是偶函数,∴-2a=0,解得a=0,
(2)由题意知(1,f(1))在x+y-3=0上,∴f(1)=2,
又∵(1,2)在y=f(x)上,∴2=
-a+a2-1+b ①,1 3
由f'(1)=-1,得1-2a+a2-1=-1 ②
由①②,解得a=1,b=
,8 3
∴f(x)=
x3-x2+1 3
,f′(x)=x2-2x,8 3
由f'(x)=0得x=0或x=2,
当x<0或x>2时,f'(x)>0;当0<x<2时,f'(x)<0;
∴函数y=f(x)的减区间为(0,2),增区间为(-∞,0),(2,+∞),
∴x=0或x=2是f(x)的极值点.
∵f(0)=
,f(2)=8 3
,f(-2)=-4,f(4)=8,4 3
∴f(x)在区间[-2,4]上的最大值为8.
(3)∵函数f(x)在区间(-1,1)不单调,∴以函数f'(x)在(-1,1)存在零点.
由f'(x)=0得,x2-2ax+a2-1=0,解得x=a-1或x=a+1,则区间长为2,
∴在区间(-1,1)上不可能有2个零点,即f'(x)在(-1,1)只有一个零点.
则f'(-1)f'(1)<0,即a2(a+2)(a-2)<0,
∵a2>0,∴(a+2)(a-2)<0,解得-2<a<2.
又由a≠0,a的取值范围为(-2,0)∪(0,2).

 mgtgθ
mgtgθ mgsinθ
mgsinθ