阅读理解。
Alice: Hi, Jerry, I heard you have fun with Peggy in Merry Park yesterday.
Jerry: Yes. We had a great time there. Why didn't you come with us? We got there by bus in
only ten minutes.
Alice: I know, but the ticket is more expensive on the weekend. Also, I've been there many times
since it opened five years ago. Did you try the Dandelion Seat there? It's so popular that people
have to wait for over an hour to get a ride.
Jerry: You mean those flower-like umbrellas that fly high in the sky?
Alice: Yes. I enjoyed riding on the Dandelion Seat and looking over the city. It was a great experience.
Jerry: Eh… I liked taking the train to get around the park better. I don't think it's fun to ride in the air.
I'd feel like I could fall down any time.
Alice: Maybe you would like it more at night. It's wonderful to see the beautiful lights below your feet.
Jerry: Well… I'm afraid of high places.
Alice: Oh, I see. That's too bad.
1. What can we learn about Merry Park?
A. It is newly opened.
B. It is also open at night.
C. It is across from Jerry's house.
D. It has the same ticket price every day.
2. What may the Dandelion Seat look like?
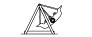
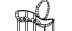
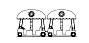
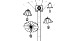
A B C D
3. Which is NOT true?
A. Alice went to Merry Park before.
B. Jerry enjoyed going around Merry Park by train.
C. Jerry would like to try the Dandelion Seat next time.
D. Jerry and Peggy went to Merry Park on the weekend.



