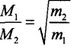问题
解答题
| 已知抛物线y=x2-2x+n与x轴交于不同的两点A,B,与y轴的交点在x轴的上方,其顶点是C. (1)求实数n的取值范围; (2)求顶点C的坐标; (3)求线段AB的长; (4)当AB=
|
答案
(1)令x2-2x+n=0,由题意知,方程x2-2x+n=0有两不等实根,
∴△=b2-4ac=(-2)2-4n>0
解得,n<1.
∵抛物线与y轴交点在x轴上方,
∴n>0.
∴n的取值范围是0<n<1.(2分)
(2)由顶点坐标公式xc=-
=1,yc=b 2a
=n-1,4ac-b2 4a
∴顶点坐标公式为C(1,n-1);(3分)
(3)由于A,B在x轴上,令x2-2x+n=0,
∵x=1±
,n
∴∠ACB=90°,
∴AB=2
(4分)1-n
(4)依题意,得2
=1-n 2
解得,n=
(5分)1 2
∴抛物线的解析式为:y=x2-2x+
(6分)1 2