问题
选择题
已知 f(x)为R上的可导函数,且f(x)<f'(x)和f(x)>0对于x∈R恒成立,则有( )
A.f(2)<e2-f(0),f(2010)>e2010-f(0)
B.f(2)>e2-f(0),f(2010)>e2010-f(0)
C.f(2)<e2-f(0),f(2010)<e2010-f(0)
D.f(2)<e2-f(0),f(2010)<e2010-f(0)
答案
∵f(x)<f'(x) 从而 f'(x)-f(x)>0 从而
>0ex[f′(x)-f(x)] e2x
从而 (
)′>0 从而函数y=f(x) ex
单调递增,故 x=2时函数的值大于x=0时函数的值,f(x) ex
即
>f(0)所以f(2)>e2f(0),f(2010)>e2010f(0).f(2) e2
故选B.

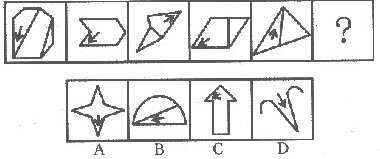 ()
()