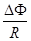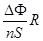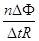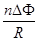问题
解答题
已知函数f(x)=x3-x2-x.
(1)求函数f(x)的单调区间;
(2)求曲线y=f(x)在点P(-1,f(-1))处的切线方程.
答案
(本小题满分14分)
(1)函数f(x)的定义域为(-∞,+∞).(1分)f′(x)=3x2-2x-1=3(x+
)(x-1).(4分)1 3
当x∈(-∞,-
)时,f'(x)>0,此时f(x)单调递增; (5分)1 3
当x∈(-
,1)时,f'(x)<0,此时f(x)单调递减; (6分)1 3
当x∈(1,+∞)时,f'(x)>0,此时f(x)单调递增.(7分)
所以函数f(x)的单调增区间为(-∞,-
)与(1,+∞),单调减区间为(-1 3
,1).(9分)1 3
(2)因为f(-1)=(-1)3-(-1)2+1=-1,(10分)f'(-1)=3×(-1)2-2×(-1)-1=4,(12分)
所以所求切线方程为y+1=4(x+1),即y=4x+3.(14分)

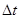 时间内穿过每匝线圈的磁通量变化为
时间内穿过每匝线圈的磁通量变化为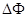 ,则通过导线某一截面的电荷量为
,则通过导线某一截面的电荷量为