问题
填空题
在四面体ABCD中,设AB=1,CD=2且AB⊥CD,若异面直线AB与CD间的距离为2,则四面体ABCD的体积为______.
答案
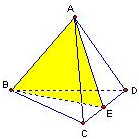
∵AB垂直于CD,
∴可以过AB作平面α,使平面α与线段CD垂直.
这样α将四面体剖成两个小的四面体.
将截面视为底,CD视为两个四面体高的总和,
那么两个小四面体的体积之和即为四面体ABCD的体积:
V=
×(1 3
×2×1)×2=1 2 2 3
故答案为:
.2 3
