问题
解答题
已知f(x)=
(1)当a=1时,求曲线y=f(x)在点(2,f(2))处的切线方程; (2)若f(x)在区间[-1,1]上是增函数,求实数a的取值范围A; (3)在(2)的条件下,设关于x的方程f(x)=
|
答案
(1)∵f(x)=
(x∈R),2x-a x2+2
∴a=1时,f(x)=
,2x-1 x2+2
∴f′=
,-2(x2-x-2) (x2+2)2
∴f′(2)=0,f(2)=
=4-1 4+2
,1 2
∴过(2,f(2))切线方程为y=
.1 2
(2)∵f(x)=
(x∈R),2x-a x2+2
∴f′(x)=
=4+2ax-2x2 (x2+2)2
,-2(x2-ax-2) (x2+2)2
∵f(x)在区间[-1,1]上是增函数,
∴f′(x)≥0对x∈[-1,1]恒成立,
即x2-ax-2≤0对x∈[-1,1]恒成立.
设g(x)=x2-ax-2,则问题等价于
,解得-1≤≤1.g(1)=1-a-2≤0 g(-1)=1+a-2≤0
∴A=[-1,1].
(3)由
=2x-a x2+2
,得x2-ax-2=0,1 x
∵△=a2+8>0,
∴x1,x2是方程x2-ax-2=0的两个非零实数根,
∴x1+x2=a,x1x2=-2,
从而|x1-x2|=
≤3,a2+8
∴不等式m2+tm+1≥|x1-x2|对任意x∈A及t∈[-1,1]恒成立.
∴m2+tm+1≥3对任意t∈[-1,1]恒成立,
∴m2+tm-2≥0对任意t∈[-1,1]恒成立,
设g(t)=m2+tm-2=mt+(m2-2),则问题等价于:
,g(-1)=m2-m-2>0 g(1)=m2+m-2≥0
解得m≤-2,或m≥2.
∴m的取值范围是(-∞,-2]∪[2,+∞).

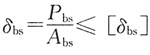 中,Abs是指连接件的()。
中,Abs是指连接件的()。