问题
填空题
一个球与正四面体的六条棱都相切,若正四面体的棱长为a,则这个球的体积是______.
答案
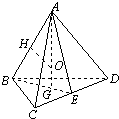
取球心O,则O与任一棱的距离即为球的半径.
如图,设CD的中点为E,底面的中心为G,
则AG⊥底面BCD,AE=BE=
a,3 2
AG=
a,AO=6 3
a,BG=6 4
a,3 3
由Rt△ABG∽Rt△AOH,
∴AB:AO=BG:OH.
∴OH=
=AO?BG AB
a.2 4
∴V=
πr3=4 3
πa3.2 24
故答案为
πa3..2 24
