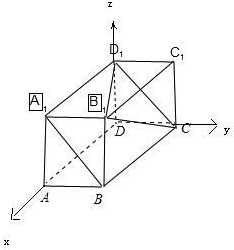
以DA为x轴，以DC为y轴，以DD₁为z轴，建立空间直角坐标系，

∵长方体ABCD-A₁B₁C₁D₁中，AB=4，AD=5，AA₁=3，

∴A₁（5，0，3），B（5，4，0），D₁（0，0，3），B₁（5，4，3），

∴

A1D1

 =(-5，0，0)，

A1B

=(0，4，-3)，

设平面A₁BCD₁的法向量为

n

=(x，y，z)，

则

-5x=0 4y-3z=0

，∴

n

=(0，3，4)，

∵

A1B1

=（0，4，0），

∴点B₁到平面A₁BCD₁的距离d=

|0+12+0|

0+9+16

=

12

5

，

长方体ABCD-A₁B₁C₁D₁中，AB=4，AD=5，AA₁=3，

∴A1B=

AA12+AB2

=

9+16

=5，

∴S_四边形A1BCD₁=A₁D₁×A₁B=5×5=25，

∴四棱锥B₁-A₁BCD₁的体积V_四棱锥B1-A₁BCD₁=

1

3

×S四边形A1BCD1×

12

5

=

1

3

×25×

12

5

=20．

故选B．