对于任意两个二次函数：y1=a1x2+b1x+c1，y2=a2x2+b2x+c2，(a1a2≠0)，当|a1|=|a2| 时，我们称这两个二次函数的图象为全等抛物线．
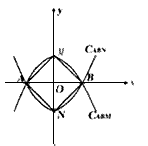
现有△ABM，A(- l，0)，B(1，0)．记过三点的二次函数抛物线为“C□□□”(“□□□”中填写相应三个点的字母)
（1）若已知M(0，1)，△ABM≌△ABN．请通过计算判断CABM与CABN是否为全等抛物线；
（2）在图中，以A、B、M三点为顶点，画出平行四边形．
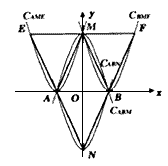
①若已知 M(0， n)，求抛物线CABM的解析式，并直接写出所有过平行四边形中三个顶点且能与CABM全等的抛物线解析式．
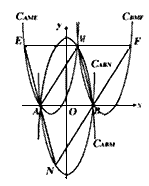
②若已知M(m，n)，当m，n满足什么条件时，存在抛物线CABM?根据以上的探究结果，判断是否存在过平行四边形中三个顶点且能与CABM全等的抛物线，若存在，请列出所有满足条件的抛物线“C□□□”；若不存在，请说明理由。
（1）解：设抛物线CABM的解析式为 y=ax2+bx+c
抛物线CABM过点A，B，M得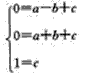 
解得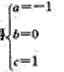
∴CABM的解析式为y=-x2+1
同理得CABN的解析式为y=x2-1
∵|1|=|-1|
∴CABM与CABN是全等抛物线；
（2）①解：设抛物线CABM的解析式为 y=ax2+bx+c
抛物线CABM过点A，B，M得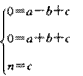 
解得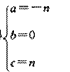
∴CABM的解析式为y=-nx2+n
与它全等的抛物线有y=nx2+n，y=n(x-1)2，y=n(x+1)2
②当n≠0且m≠±1时，存在抛物线CABM，
与CABM全等的抛物线有：CABN，CAME，CBMF
